Why do we want simpler models?

Alot of work have gone into creating as precise models of single neurons as possible, but integrate-and-fire neurons is a step in the other direction. They are much simpler than for example the Hodgkin-Huxley model. So why do we want to use a simpler model when we have an advanced one?

As it turns out there are several reasons. The following figure is the action potential generated by the Hodkin Huxley model. It has several interesting features and capture much of what happens in a neuron when it sends out a signal. But what if we want to simulate a network? Where the shape of the action potential is irrelevant and we only are interested in when the neuron spikes. And we would like to evaluate a lage number of neurons

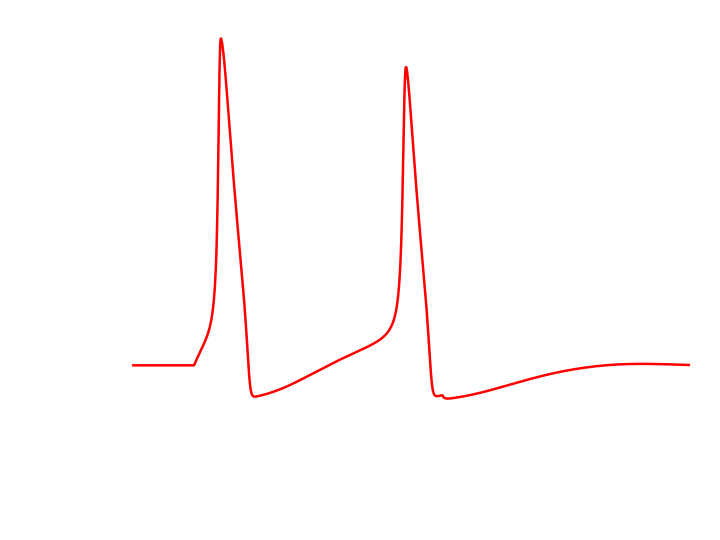
The Hodkin-Huxley model takes time to evaluate for each neuron and the same is the case with more advanced models. A mouse has 10-20 million neurons while a human has ~100 million neurons. If we have a faster model than the Hodgkin-Huxley model that perhaps saves 1 second computation time for each neuron when simulating the 100 million neurons in a human, we save a total if 3.2 years, not to mention problems with RAM and so on. It must be mentiond we are far from capable of simulating that many neurons at the current stage. In a network we are also only interested in when a neuron spikes, and not the detailed shape of the action potential. So we do not need all the information we get from the more detailed models. Meaning that we do not lose much precission by removing complexity from our model. These two facts, that we need a neuron that is faster to evaluate and that we don't have any interest in other than when the neuron spikes are the two main reasons why we want simpler models.

In addition to this, it is not certain that more detailed models are more realistic. A more detalied model means more parameters, and many of thesemodel parameters are unknown, in addition to varying with time, introducing uncertainties that we avoid with a simpler model. As such, a simpler model is "more real". Describe neural models with a bare minimum of features alos exposes the core mechanisms of what is behind the phenomena.

The integrate-and-fire neurons

One of the better examples of a simplified neuronal model is the integrate-and-fire neuron, which is a simple spike generating neuron. The idea is that we only want to know when the neuron spikes and do not care about anything else. To achive this we sett a threshold, \(\theta\), and when the membrane potential reaches this value we say that the neuron spikes and reset the potential back to the resting potential

The spikes are manually added.

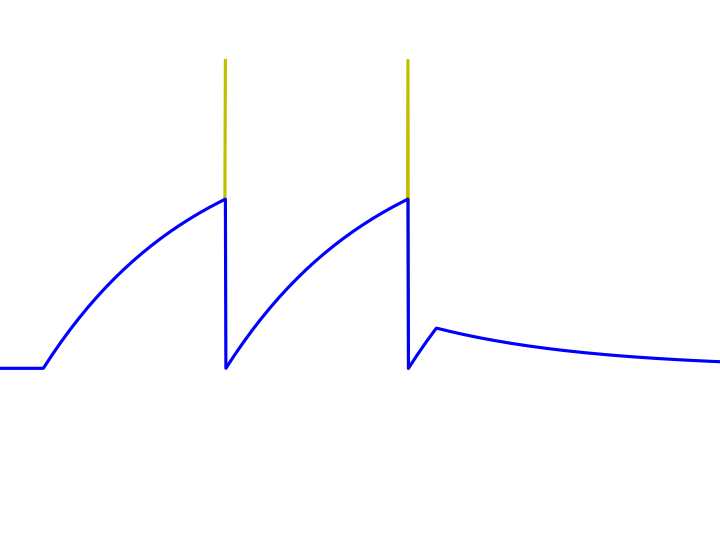
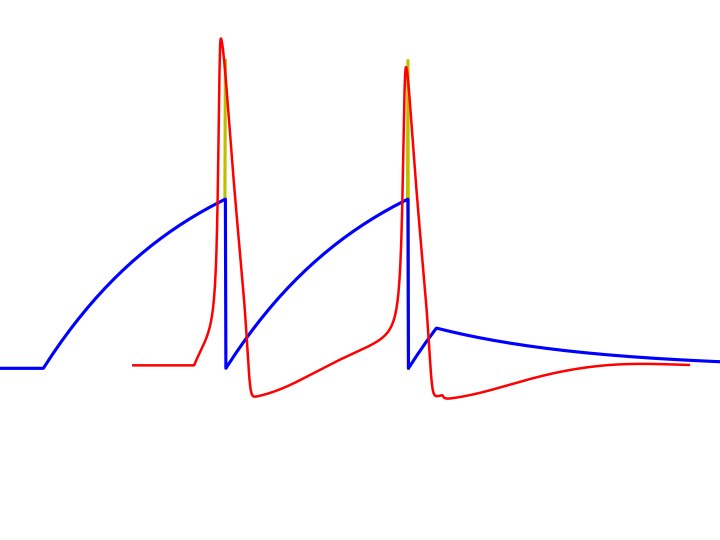
We can compare this with the Hodgkin-Huxley model. We see that we have much less details, but the only thing we are interested in, when the neuron spikes, is the same for both models.

Modeling integrate-and-fire neurons

The integrate-and-fire neuron is modelled as a simple RC circuit with spike generation and a reset mechanism added.

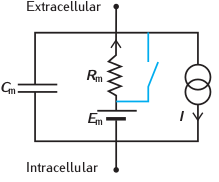
Using Kirchoff's law we get

\(I_C + I_R = I\)

where \( I_C\) is the current through the capacitance, \(I_R\) the current through the resistance and \(I\) the injected current.

Using ohms law with driving force we get

\(V-E_m = RI_R\)

\(I_R = \frac{V-E_m}{R} \)

where \(E_m\) is the reversial potenital. This gives

\(I_C = - \frac{V-E_m}{R} + I \)

For a capacitance we have \(q = C_mV\) where \(C_m\) is the membrane capacitance. Using the definition of a current

\(I = \frac{dq}{dt}\)

we get

\(\frac{dq_C}{dt} = - \frac{V-E_m}{R} + I \)

\(\frac{dC_mV}{dt} = - \frac{V-E_m}{R} + I \)

when the capacitance is constant we get the final equation for a integrate-and-fire neuron

\(C_m\frac{dV}{dt} = - \frac{V-E_m}{R} + I \)

This is the central differential equation in neuronify, which is trivial. The change in voltage per timestep is

\( dV = - \frac{V-E_m}{C_mR}*dt + \frac{I}{C_m}*dt \)

How is spiking achieved and threated?

It is achived by having a threshold value \(\theta\) (default it is 0 mV, but can be adjusted) and when the membrane potential reaches this threshold a spike is generated. This creates a fire event that tells the neurons connected to the firing neuron that the firing neuron is firing. The membrane potential in the firing neuron is set to 100, before it is reset back to the resting potential and the conductance is set to 0.