In integrate-and-fire models we are often interested in feeding our model network with spike input representing a large unknown part of the network rather than simple current generators. In Neuronify, we have added the possibility of doing this by a spike generator, which generates spikes which follow a Poisson distribution.

Spike generators

When investigating properties of a single neuron, a DC or AC generator is useful for providing input to the neuron. However, in networks in vivo, there are no such generators, and networks are driven by input from other areas of the brain. Such input can be modeled by rate models, where we know the average amount of spikes coming from the unknown network. A successful example of such a network model is given in [1], where they simulate a fairly large network (much larger than the intended scope for Neuronify).

Poisson distribution

A Poisson distribution, named after the French mathematician Simeon Denis Poisson, is a discrete probability distribution that expresses the probability of a given number of events occuring in a fixed time interval if the events are independent and have a known rate. Many processes approximately follow this description, such as the amount of letters received in a mailbox per day or the amount of cars on a highway passed under a bridge in a 5-minute interval. This is also a reasonable approximation for synaptic input from a large number of neurons.

The probability function for a Poisson process is given by

\[ Pr(X=n) = f(n) = \frac{\lambda^n e^{-\lambda }}{n!}, \]

and one can check that both the expected value and variance of \(X\) is \(\lambda\) .

Implementation

The expected number of spikes, \( \lambda \) in a time step in neuronify is related to the rate \( r \) as

\[ \lambda = r \, \Delta t \]

where \( \Delta t \) is the size of the time step.

There are two common ways of modeling such a process. One can find all the spike times in advance by modeling the time between successive spikes. This can be done by drawing the time to the first spike from an exponential distribution. Then, the time between the first and second spike time can be drawn in the same way, and so on.

A simpler way of modeling a Poisson process is to choose whether or not there is an event for each time step. This can be done by drawing a random number \( x \)in the interval \( [0,1] \). If \( r \Delta t > x \) the spike is fired, otherwise it is not. This is the model implemented in Neuronify. For more details, see [2].

Limitations and Drawbacks

The simple implementation has a limitation in that if \( r\Delta t > 1 \) the generator will always fire, but it will still not fire the expected number of spikes. In addition, since this model only permits one spike per time step we might miss some spikes even for even smaller \( r \). For this model to be reasonable, we should require \( P(X > 1) \) to be very small.

Example: Noise

Noise can make a neuron fire even when the basic input is not sufficient to bring it above threshold. In this example we begin by creating a neuron and connecting a dc generator to it. The generator is set just at subthreshold output.

We can make add noise to a neuron by adding Poisson generators. We can add two Poisson generators to the canvas. Set their rates to 2.0 ms\( ^{-1} \) and their stimulation output to 0.1, and make one of the generators inhibitory. The network should look like the following:

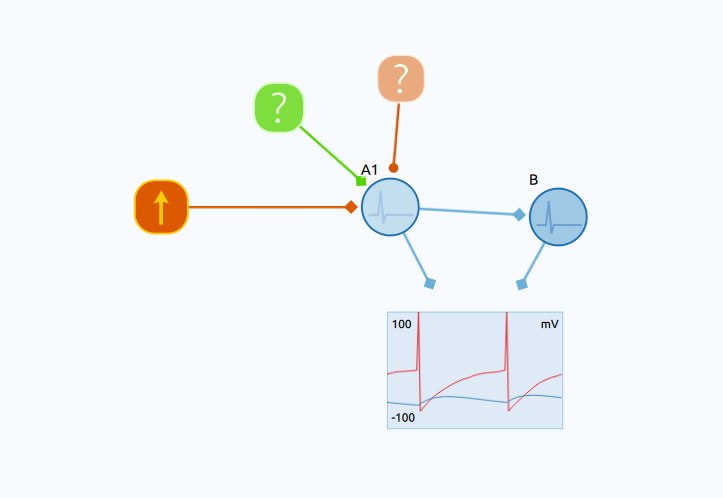
References

[1] Nicolas Brunel. Dynamics of Sparsely Connected Networks of Excitatory and Inhibitory Spiking Neurons. Journal of Computational Neuroscience 8, 183-208, 2000.

[2] Dayan and Abbott. Theoretical Neuroscience. 2000